Λέοναρντ Όιλερ

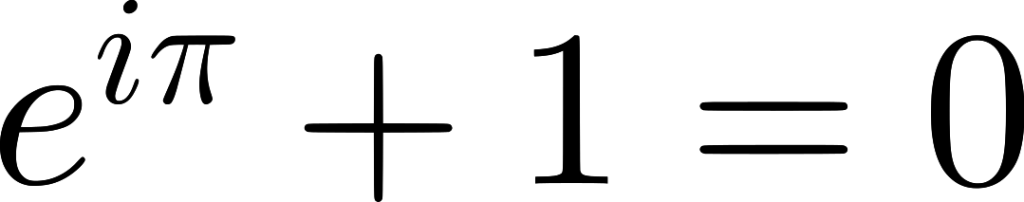
Ο Euler μπορεί να είναι ο μαθηματικός με τη μεγαλύτερη επιρροή που έζησε ποτέ (αν και κάποιοι θα τον θεωρούσαν δεύτερο μετά τον Ευκλείδη). κατατάσσεται #77 στη διάσημη λίστα του Μάικλ Χαρτ με τα Πρόσωπα με τη μεγαλύτερη επιρροή στην Ιστορία. Οι συνάδελφοί του τον αποκαλούσαν «Ενσαρκωμένη Ανάλυση». Ο Laplace, διάσημος επειδή αρνήθηκε τα εύσημα σε άλλους μαθηματικούς, είπε κάποτε «Διαβάστε τον Euler: είναι ο δάσκαλός μας σε όλα». Οι σημειώσεις και οι μέθοδοί του σε πολλούς τομείς χρησιμοποιούνται μέχρι σήμερα. Ο Euler ήταν ο πιο παραγωγικός μαθηματικός στην ιστορία. Μερικοί μελετητές κατατάσσουν την “Introductio in analysin infinitorum” του 1748 πάνω από τη “Géométrie” του Ντεκάρτ, τις “Disquisitiones” του Γκάους, ακόμη και το “Principia Mathematica” του Νεύτωνα.

Όπως ο Αρχιμήδης επέκτεινε τη γεωμετρία του Ευκλείδη, έτσι και ο Όιλερ εκμεταλλεύτηκε θαυμάσια την ανάλυση του Νεύτωνα και του Λάιμπνιτς. Έδωσε επίσης στον κόσμο τη σύγχρονη τριγωνομετρία. Πρωτοστάτησε (μαζί με τον Lagrange) στον λογισμό των παραλλαγών. Γενίκευσε και απέδειξε τους τύπους Newton-Giraud και είχε σημαντική συνεισφορά στην άλγεβρα, π.χ. η μελέτη του για τις υπεργεωμετρικές σειρές. Ήταν επίσης άριστος στα διακριτά μαθηματικά, εφευρίσκοντας τη θεωρία γραφημάτων. Ο Euler έγραψε την πρώτη οριστική πραγματεία για τα συνεχή κλάσματα, καθιερώνοντας πολλά βασικά θεωρήματα για αυτό το σημαντικό θέμα. Αν και η εφεύρεση της δημιουργίας συναρτήσεων αποδίδεται στον DeMoivre, ο Euler εκμεταλλεύτηκε εξαιρετικά την ιδέα: για παράδειγμα, αφήνοντας το p(n) να υποδηλώνει τον αριθμό των διαμερίσεων του n, ο Euler βρήκε την υπέροχη εξίσωση:

$\sum _n {p(n)x^n}=\dfrac{1}{\Pi_k}(1-x^k)$

Ο Euler βρήκε μια έξυπνη απόδειξη γι’ αυτό που τώρα ονομάζεται “μια από τις πιο βαθιές ανακαλύψεις του”, σχετική με τη θεωρία των ελλειπτικών αρθρωτών συναρτήσεων.

Ο Euler ήταν ένας πολύ σημαντικός στη θεωρία αριθμών. Απέδειξε ότι το άθροισμα των αντίστροφων πρώτων αριθμών αποκλίνει (και είναι περίπου ln (ln (p)) αν αθροιστούν οι πρώτοι αντίστροφοι μέχρι το 1/p). Εφηύρε τη συνάρτηση “Φ” και τη χρησιμοποίησε για να γενικεύσει το Μικρό Θεώρημα του Φερμά, βρήσκοντας τόσο τον μεγαλύτερο τότε γνωστό πρώτο όσο και τον μεγαλύτερο τότε γνωστό τέλειο αριθμό, απέδειξε ότι ο e είναι άρρητος, ανακάλυψε (αν και χωρίς πλήρη απόδειξη) μια ευρεία κατηγορία υπερβατικών αριθμών , απέδειξε ότι όλοι οι ακόμη τέλειοι αριθμοί πρέπει να έχουν την αριθμητική μορφή Mersenne που είχε ανακαλύψει ο Ευκλείδης 2000 χρόνια νωρίτερα, και πολλά άλλα. Ο Euler ήταν επίσης πρώτος που απέδειξε αρκετά ενδιαφέροντα θεωρήματα γεωμετρίας, σχέσεις μεταξύ των υψών ενός τριγώνου, των διαμέσου και των περιγραμμένων και εγγεγραμμένων κύκλων. Το περίφημο Θεώρημα Διασταυρωμένων Χορδών. και μια έκφραση για τον όγκο ενός τετραέδρου ως προς τα μήκη των ακμών του. Ο Euler ήταν ο πρώτος που εξερεύνησε την τοπολογία, αποδεικνύοντας θεωρήματα για τη χαρακτηριστική του Euler, και το περίφημο πολυεδρικό θεώρημα του Euler, F+V = E+2 (αν και μπορεί να ανακαλύφθηκε από τον Descartes και να αποδείχθηκε για πρώτη φορά αυστηρά από τον Jordan). Αν και σημειώθηκε ως ο πρώτος μεγάλος «καθαρός μαθηματικός», οι εξισώσεις αντλίας και στροβίλου του Euler έφεραν επανάσταση στο σχεδιασμό των αντλιών. Έκανε επίσης σημαντική συμβολή στη θεωρία της μουσικής, την ακουστική, την οπτική, τις ουράνιες κινήσεις, τη δυναμική των ρευστών και τη μηχανική. Επέκτεινε τους Νόμους της Κίνησης του Νεύτωνα σε περιστρεφόμενα άκαμπτα σώματα. και ανέπτυξε την εξίσωση δέσμης Euler-Bernoulli. Σε μια πιο ελαφριά νότα, ο Euler κατασκεύασε ένα ιδιαίτερα «μαγικό» μαγικό τετράγωνο.

Ο Euler πιστώνεται με την πρώτη απόδειξη του Θεωρήματος των Χριστουγέννων του Fermat (ένας πρώτος της μορφής 4k+1 είναι το άθροισμα δύο τετραγώνων με έναν ακριβώς τρόπο). Στον Euler πιστώνονται τουλάχιστον τέσσερα από τα “Δέκα πιο όμορφα θεωρήματα” που επιλέχθηκαν από ένα περιοδικό μαθηματικών. Σε μια ξεχωριστή λίστα (“Εκατό πιο σημαντικά θεωρήματα”) που προετοιμάστηκε για ένα συνέδριο για τα μαθηματικά το 1999, ο Euler πιστώνεται με επτά από τα θεωρήματα, πολύ πιο μπροστά από οποιονδήποτε άλλο εκτός από τον Ευκλείδη.

Ο Euler συνδύασε τη λάμψη του με την εκπληκτική συγκέντρωση. Ανέπτυξε την πρώτη μέθοδο για να εκτιμήσει την τροχιά της Σελήνης (το πρόβλημα των τριών σωμάτων που είχε απασχολήσει τον Νεύτωνα) και διευθέτησε μια αριθμητική διαμάχη που περιελάμβανε 50 όρους σε μια μακρά συγκλίνουσα σειρά. Και τα δύο αυτά κατορθώματα επιτεύχθηκαν όταν ήταν εντελώς τυφλός. (Σχετικά με αυτό είπε “Τώρα θα έχω λιγότερο περισπασμό.”) Ο Φρανσουά Αραγκό είπε ότι “Ο Όιλερ υπολόγιζε χωρίς εμφανή προσπάθεια, όπως οι άνθρωποι αναπνέουν ή όπως οι αετοί συντηρούνται στον άνεμο.”

Τέσσερα από τα πιο σημαντικά σύμβολα σταθερών στα μαθηματικά (π, e, i = √-1, και γ = 0,57721566…) εισήχθησαν όλα ή διαδόθηκαν από τον Euler, μαζί με τελεστές όπως ο (Σ). Έκανε σημαντική δουλειά με τη συνάρτηση ζήτα του Riemann (αν και τότε δεν ήταν γνωστή με αυτό το όνομα). Ο Euler ξεκίνησε ως νεαρός μαθητής της οικογένειας Bernoulli και ήταν συγκάτοικος του Daniel Bernoulli στην Αγία Πετρούπολη, όπου ο Euler προσλήφθηκε για πρώτη φορά ως δάσκαλος φυσιολογίας. Όμως, στην ηλικία των είκοσι οκτώ, ο Euler ανακάλυψε την εντυπωσιακή ταυτότητα

$\zeta(2)=\dfrac{\pi^2}{6}$

Αυτό έκανε τον Euler να αποκτήσει αμέσως φήμη. Ο Euler και άλλοι ανέπτυξαν εναλλακτικές αποδείξεις και γενικεύσεις αυτού του «προβλήματος της Βασιλείας», και φυσικά η συνάρτηση ζ (ζήτα) είναι πλέον πολύ διάσημη. Μεταξύ πολλών άλλων διάσημων και σημαντικών ταυτοτήτων, ο Euler απέδειξε το Πεντάγωνο Θεώρημα Αριθμών και τον τύπο

$\zeta(s)=\Pi (1-p^{-s})^{-1}$

Αυτή η φόρμουλα προϊόντος οδηγεί απευθείας στο θεώρημα των πρώτων αριθμού του Riemann, με τη σχετική υπόθεση Riemann.

Ακόμη πιο διάσημη είναι η ταυτότητα (την οποία ο Richard Feynman αποκάλεσε «σχεδόν εκπληκτικό… κόσμημα») που ενοποιεί τις τριγωνομετρικές και εκθετικές συναρτήσεις

$e^{i x}=\cos(x)+i\sin(x)$

Και είναι σχεδόν θαυμαστό πώς η συγκεκριμένη εξίσωση

$e^{i\pi}+1=0$

συνδυάζει τις πιο σημαντικές σταθερές μαζί.

Published by

Θεμιστοκλής Παπαβραμίδης