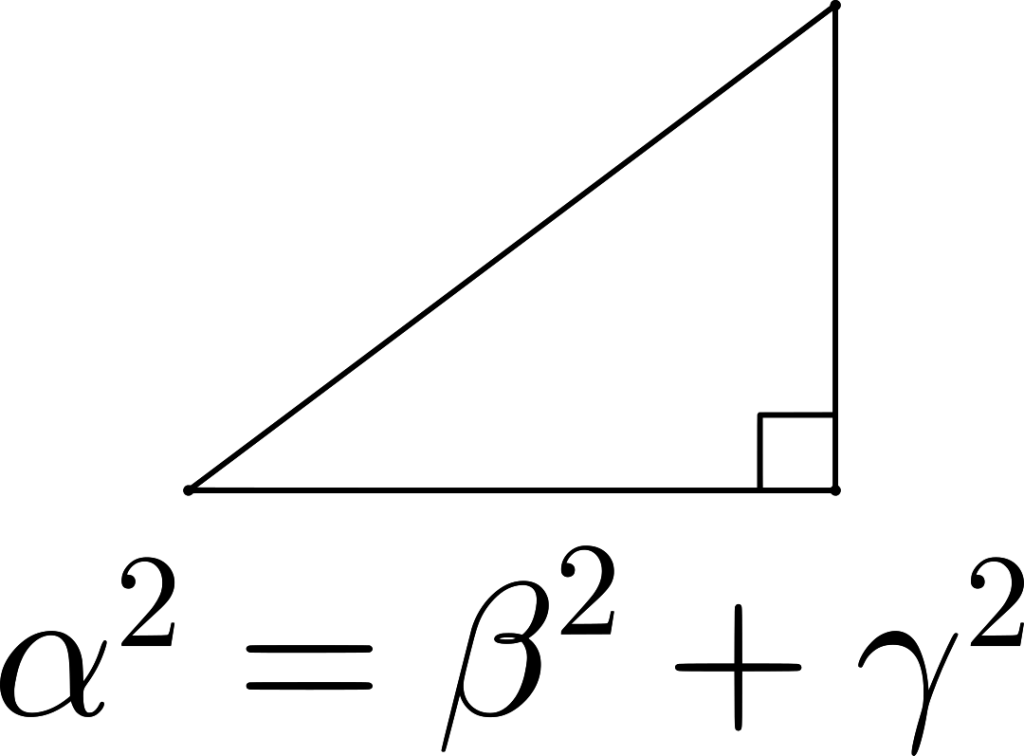Καθώς η ελληνική αυτοκρατορία άρχισε να εξαπλώνει τη σφαίρα επιρροής της στη Μικρά Ασία, τη Μεσοποταμία και όχι μόνο, οι Έλληνες ήταν αρκετά έξυπνοι ώστε να υιοθετήσουν και να προσαρμόσουν χρήσιμα στοιχεία από τις κοινωνίες που κατέκτησαν. Αυτό ίσχυε για τα μαθηματικά τους όσο οτιδήποτε άλλο, και υιοθέτησαν στοιχεία μαθηματικών τόσο από τους Βαβυλώνιους όσο και από τους Αιγύπτιους. Σύντομα όμως άρχισαν να κάνουν σημαντικές συνεισφορές από μόνοι τους και, για πρώτη φορά, μπορούμε να αναγνωρίσουμε τις συνεισφορές μεμονωμένων ατόμων. Μέχρι την ελληνιστική περίοδο, οι Έλληνες είχαν προεδρεύσει σε μια από τις πιο δραματικές και σημαντικές επαναστάσεις στη μαθηματική σκέψη όλων των εποχών.
Αττικοί ή Ηρωδιανικοί αριθμοί
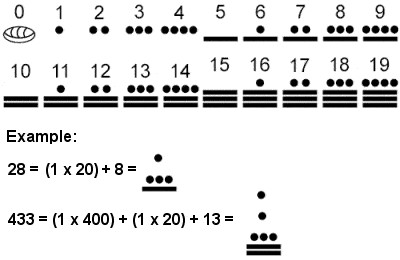
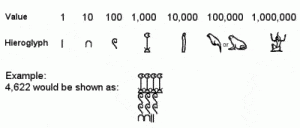
Το αρχαίο ελληνικό αριθμητικό σύστημα, γνωστό ως Αττικοί ή Ηρωδιανικοί αριθμοί, αναπτύχθηκε πλήρως περίπου το 450 π.Χ. και ήταν σε γενική χρήση πιθανώς ήδη από τον 7ο αιώνα π.Χ. Ήταν ένα σύστημα βάσης 10 παρόμοιο με το προηγούμενο αιγυπτιακό (και ακόμη πιο παρόμοιο με το μεταγενέστερο ρωμαϊκό σύστημα), με σύμβολα για 1, 5, 10, 50, 100, 500 και 1.000 επαναλαμβανόμενα όσες φορές χρειαζόταν για να αναπαραστήσουν τον επιθυμητό αριθμό. Η πρόσθεση έγινε αθροίζοντας χωριστά τα σύμβολα (1, 10, 100, κ.λπ.) στους αριθμούς που έπρεπε να προστεθούν και ο πολλαπλασιασμός ήταν μια επίπονη διαδικασία βασισμένη σε διαδοχικούς διπλασιασμούς (η διαίρεση βασίστηκε στο αντίστροφο αυτής της διαδικασίας).
Το θεώρημα του Θαλή
Τα περισσότερα ελληνικά μαθηματικά βασίστηκαν στη γεωμετρία. Ο Θαλής, ένας από τους Επτά Σοφούς της Αρχαίας Ελλάδας, που έζησε στις ακτές του Ιονίου της Μικράς Ασίας το πρώτο μισό του 6ου αιώνα π.Χ., θεωρείται συνήθως ο πρώτος που έθεσε κατευθυντήριες γραμμές για την αφηρημένη ανάπτυξη της γεωμετρίας, αν και αυτό που γνωρίζουμε για το έργο του (όπως για όμοια και ορθογώνια τρίγωνα) φαίνεται τώρα αρκετά στοιχειώδες.
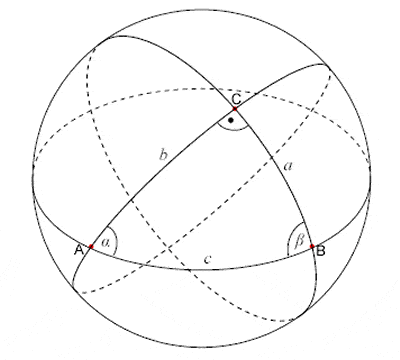
Ο Θαλής καθιέρωσε το θεώρημα σύμφωνα με το οποίο εάν ένα τρίγωνο σχεδιαστεί μέσα σε έναν κύκλο με τη μεγάλη πλευρά ως διάμετρο του κύκλου, τότε η απέναντι γωνία θα είναι πάντα ορθή (καθώς και κάποιες άλλες σχετικές ιδιότητες που προκύπτουν από αυτό). Του πιστώνεται επίσης ένα άλλο θεώρημα, γνωστό ως Θεώρημα του Θαλή, σχετικά με τους λόγους των τμημάτων που δημιουργούνται εάν δύο ευθείες τέμνονται από τρεις παράλληλες.
Σε κάποιο βαθμό, ωστόσο, ο θρύλος του μαθηματικού του 6ου αιώνα π.Χ., Πυθαγόρα του Σάμιου, έχει γίνει συνώνυμος με τη γέννηση των ελληνικών μαθηματικών. Πράγματι, πιστεύεται ότι επινόησε και τις δύο λέξεις «φιλοσοφία» («αγάπη για τη σοφία») και «μαθηματικά» («αυτό που μαθαίνεται»). Ο Πυθαγόρας ήταν ίσως ο πρώτος που συνειδητοποίησε ότι μπορούσε να κατασκευαστεί ένα πλήρες σύστημα μαθηματικών, όπου τα γεωμετρικά στοιχεία αντιστοιχούσαν με αριθμούς. Το Θεώρημα του Πυθαγόρα (ή το Πυθαγόρειο Θεώρημα) είναι ένα από τα πιο γνωστά από όλα τα μαθηματικά θεωρήματα. Παραμένει όμως μια αμφιλεγόμενη φιγούρα, όπως θα δούμε, και τα ελληνικά μαθηματικά σε καμία περίπτωση δεν περιορίζονταν σε έναν άνθρωπο.
Τρία γεωμετρικά προβλήματα
Τρία γεωμετρικά προβλήματα συγκεκριμένα, που συχνά αναφέρονται ως Τρία Κλασικά Προβλήματα, και όλα πρέπει να επιλυθούν με καθαρά γεωμετρικά μέσα χρησιμοποιώντας μόνο μια ευθεία ακμή και έναν διαβήτη, χρονολογούνται από τις πρώτες μέρες της ελληνικής γεωμετρίας: «Ο τετραγωνισμός του κύκλου», «ο διπλασιασμός του κύβου» και «η τριχοτόμιση μιας γωνίας». Αυτά τα προβλήματα είχαν βαθιά επιρροή στη μελλοντική γεωμετρία και οδήγησαν σε πολλές γόνιμες ανακαλύψεις, αν και οι πραγματικές λύσεις τους (ή, όπως αποδείχθηκε, οι αποδείξεις της αδυναμίας τους) έπρεπε να περιμένουν μέχρι τον 19ο αιώνα.
Ο Ιπποκράτης ο Χίος (δεν πρέπει να συγχέεται με τον μεγάλο Έλληνα γιατρό Ιπποκράτη της Κω.) ήταν ένας τέτοιος Έλληνας μαθηματικός που ασχολήθηκε με αυτά τα προβλήματα κατά τον 5ο αιώνα π.Χ. Το έργο του αποτέλεσε σημαντική πηγή για το μεταγενέστερο έργο του Ευκλείδη.
Το Παράδοξο του Ζήνωνα και του Αχιλλέα και της Χελώνας
Οι Έλληνες ήταν αυτοί που πρώτοι καταπιάστηκαν με την ιδέα του απείρου, όπως περιγράφεται στα γνωστά παράδοξα που αποδίδονται στον φιλόσοφο Ζήνωνα από την Ελέα τον 5ο αιώνα π.Χ. Το πιο διάσημο από τα παράδοξά του είναι αυτό του Αχιλλέα και της Χελώνας, που περιγράφει έναν θεωρητικό αγώνα ανάμεσα στον Αχιλλέα και μια χελώνα. Ο Αχιλλέας δίνει στην πολύ πιο αργή χελώνα ένα προβάδισμα, αλλά όταν ο Αχιλλέας φτάσει στο σημείο εκκίνησης της χελώνας, η χελώνα έχει ήδη προχωρήσει. Μέχρι να φτάσει ο Αχιλλέας σε αυτό το σημείο, η χελώνα έχει προχωρήσει ξανά, κτλ, κτλ, έτσι ώστε κατ ‘αρχήν ο γρήγορος Αχιλλέας δεν μπορεί ποτέ να προλάβει την αργή χελώνα.
Παράδοξα όπως αυτό και το λεγόμενο Παράδοξο Διχοτομίας του Ζήνωνα βασίζονται στην άπειρη διαιρετότητα του χώρου και του χρόνου και βασίζονται στην ιδέα ότι το μισό συν ένα τέταρτο συν ένα όγδοο συν ένα δέκατο έκτο, κλπ, κλπ, στο άπειρο ίσον με ένα. Το παράδοξο, ωστόσο, πηγάζει από την εσφαλμένη υπόθεση ότι είναι αδύνατο να συμπληρωθεί ένας άπειρος αριθμός διακριτών στοιχείων σε πεπερασμένο χρόνο, αν και είναι εξαιρετικά δύσκολο να αποδειχθεί το παράδοξο. Ο αρχαίος Έλληνας Αριστοτέλης ήταν ο πρώτος από πολλούς που προσπάθησε να διαψεύσει τα παράδοξα, ιδιαίτερα καθώς πίστευε ακράδαντα ότι το άπειρο θα μπορούσε να είναι μόνο δυνητικό και όχι πραγματικό.
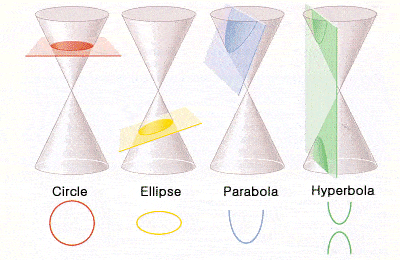
Ο Δημόκριτος, ο πιο διάσημος για τις προφητείες του σχετικά με το ότι όλη η ύλη αποτελείται από μικροσκοπικά άτομα, ήταν επίσης πρωτοπόρος των μαθηματικών και της γεωμετρίας τον 5ο – 4ο αιώνα π.Χ., και δημιούργησε έργα με τίτλους όπως «Περί αριθμών», «Γεωμετρία», αν και αυτά τα έργα δεν έχουν διασωθεί. Γνωρίζουμε ότι ήταν από τους πρώτους που παρατήρησαν ότι ένας κώνος (ή πυραμίδα) έχει το ένα τρίτο του όγκου ενός κυλίνδρου (ή πρίσματος) με την ίδια βάση και ύψος, και είναι ίσως ο πρώτος που σκέφτηκε σοβαρά τη διαίρεση αντικειμένων σε άπειρο αριθμό διατομών.
Ωστόσο, είναι βέβαιο ότι ο Πυθαγόρας επηρέασε ιδιαίτερα αυτούς που ακολούθησαν, συμπεριλαμβανομένου του Πλάτωνα, ο οποίος ίδρυσε την περίφημη Ακαδημία του στην Αθήνα το 387 π.Χ., και τον προστατευόμενό του Αριστοτέλη, του οποίου το έργο στη λογική θεωρήθηκε οριστικό για πάνω από δύο χιλιάδες χρόνια. Ο Πλάτωνας είναι περισσότερο γνωστός για την περιγραφή των πέντε πλατωνικών στερεών, αλλά η αξία του έργου του ως δάσκαλου και εκλαϊκευτή των μαθηματικών δεν μπορεί να υπερεκτιμηθεί.
Ο μαθητής του Πλάτωνα, Εύδοξος, πιστώνεται συνήθως με την πρώτη εφαρμογή της «μεθόδου εξάντλησης» (αργότερα αναπτύχθηκε από τον Αρχιμήδη), μια πρώιμη μέθοδο ολοκλήρωσης με διαδοχικές προσεγγίσεις που χρησιμοποίησε για τον υπολογισμό του όγκου της πυραμίδας και του κώνου. Ανέπτυξε επίσης μια γενική θεωρία αναλογίας, η οποία ήταν εφαρμόσιμη σε ασύμμετρα (παράλογα) μεγέθη που δεν μπορούν να εκφραστούν ως λόγος δύο ακέραιων αριθμών, καθώς και σε συγκρίσιμα (ορθολογικά) μεγέθη, επεκτείνοντας έτσι τις ημιτελείς ιδέες του Πυθαγόρα.
Ίσως η πιο σημαντική μεμονωμένη συνεισφορά των Ελλήνων ήταν η ιδέα της απόδειξης και η επαγωγική μέθοδος χρήσης λογικών βημάτων για την απόδειξη ή την απόρριψη θεωρημάτων από αρχικά υποτιθέμενα αξιώματα. Παλαιότεροι πολιτισμοί, όπως οι Αιγύπτιοι και οι Βαβυλώνιοι, βασίζονταν σε επαγωγικό συλλογισμό, που χρησιμοποιεί επαναλαμβανόμενες παρατηρήσεις για να καθορίσουν εμπειρικούς κανόνες. Αυτή η έννοια της απόδειξης είναι που δίνει στα μαθηματικά τη δύναμή τους και διασφαλίζει ότι οι αποδεδειγμένες θεωρίες είναι τόσο αληθινές σήμερα όσο πριν από δύο χιλιάδες χρόνια, και που έθεσε τα θεμέλια για τη συστηματική προσέγγιση των μαθηματικών του Ευκλείδη και όσων ήρθαν μετά από αυτόν.