Οι πρώτοι Αιγύπτιοι εγκαταστάθηκαν κατά μήκος της εύφορης κοιλάδας του Νείλου περίπου το 6000 π.Χ. και άρχισαν να καταγράφουν τα μοτίβα των σεληνιακών φάσεων και των εποχών, τόσο για γεωργικούς όσο και για θρησκευτικούς λόγους.
Οι επιθεωρητές του Φαραώ χρησιμοποίησαν μετρήσεις με βάση τα μέρη του σώματος (μια παλάμη ήταν το πλάτος του χεριού, μια πήχη η μέτρηση από τον αγκώνα μέχρι τα δάχτυλα) για να μετρήσουν τη γη και τα κτίρια πολύ νωρίς στην αιγυπτιακή ιστορία, και ένα δεκαδικό αριθμητικό σύστημα αναπτύχθηκε με βάση τα δέκα μας δάχτυλα. Ωστόσο, το παλαιότερο μαθηματικό κείμενο από την αρχαία Αίγυπτο που έχει ανακαλυφθεί μέχρι στιγμής, είναι ο Πάπυρος της Μόσχας, ο οποίος χρονολογείται από το Αιγυπτιακό Μέσο Βασίλειο περίπου το 2000 – 1800 π.Χ.
Αρχαίο Αιγυπτιακό Αριθμητικό Σύστημα
Θεωρείται ότι οι Αιγύπτιοι εισήγαγαν το αρχαιότερο πλήρως ανεπτυγμένο σύστημα αρίθμησης βάσης 10 τουλάχιστον ήδη από το 2700 π.Χ. (και πιθανώς πολύ νωρίς). Οι γραπτοί αριθμοί χρησιμοποίησαν μια κάθετη γραμμή για τις μονάδες, ένα πέταλο για δεκάδες, μια σπείρα για εκατοντάδες και ένα φυτό λωτού για χιλιάδες, καθώς και άλλα ιερογλυφικά σύμβολα για υψηλότερες δυνάμεις από δέκα έως και ένα εκατομμύριο.
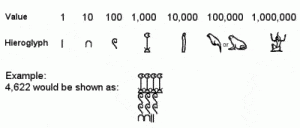
Ωστόσο, δεν υπήρχε η έννοια της αξίας θέσης, επομένως οι μεγαλύτεροι αριθμοί ήταν μάλλον δύσχρηστοι (αν και ένα εκατομμύριο απαιτούσε μόνο έναν χαρακτήρα, ένα εκατομμύριο μείον ένα απαιτούσε πενήντα τέσσερις χαρακτήρες).
Ο πάπυρος Rhind, που χρονολογείται γύρω στο 1650 π.Χ., είναι ένα είδος εγχειριδίου οδηγιών στην αριθμητική και τη γεωμετρία, και μας δίνει σαφείς επιδείξεις για το πώς γινόταν ο πολλαπλασιασμός και η διαίρεση εκείνη την εποχή. Περιέχει επίσης στοιχεία για άλλες μαθηματικές γνώσεις, συμπεριλαμβανομένων κλασμάτων μονάδας, σύνθετων και πρώτων αριθμών, αριθμητικών, γεωμετρικών και αρμονικών μέσων και πώς να λύσετε γραμμικές εξισώσεις πρώτης τάξης καθώς και αριθμητικές και γεωμετρικές σειρές. Ο Πάπυρος του Βερολίνου, που χρονολογείται γύρω στο 1300 π.Χ., δείχνει ότι οι αρχαίοι Αιγύπτιοι μπορούσαν να λύσουν αλγεβρικές εξισώσεις δευτέρου βαθμού.
Ο πολλαπλασιασμός, για παράδειγμα, επιτεύχθηκε με μια διαδικασία επαναλαμβανόμενου διπλασιασμού του αριθμού που πρέπει να πολλαπλασιαστεί στη μία πλευρά και του ενός στην άλλη, ουσιαστικά ένα είδος πολλαπλασιασμού δυαδικών παραγόντων παρόμοιων με αυτόν που χρησιμοποιείται από σύγχρονους υπολογιστές. Αυτό χρησιμοποίησε αποτελεσματικά την έννοια των δυαδικών αριθμών, πάνω από 3.000 χρόνια πριν τον εισαγάγει ο Leibniz στη Δύση, και πολλά ακόμη χρόνια πριν η ανάπτυξη του υπολογιστή ήταν να εξερευνήσει πλήρως τις δυνατότητές του.
Τα πρακτικά προβλήματα του εμπορίου και της αγοράς οδήγησαν στην ανάπτυξη μιας σημειογραφίας για τα κλάσματα. Οι πάπυροι που μας έχουν φτάσει καταδεικνύουν τη χρήση μοναδιαίων κλασμάτων με βάση το σύμβολο του ματιού του Ώρου, όπου κάθε μέρος του ματιού αντιπροσώπευε ένα διαφορετικό κλάσμα, κάθε μισό του προηγούμενου (δηλαδή μισό, τέταρτο, όγδοο, δέκατο έκτο , τριάντα δεύτερο, εξήντα τέταρτο), έτσι ώστε το σύνολο ήταν ένα εξήντα τέταρτο λιγότερο από ένα σύνολο, το πρώτο γνωστό παράδειγμα μιας γεωμετρικής σειράς.
Τα μοναδιαία κλάσματα θα μπορούσαν επίσης να χρησιμοποιηθούν για απλά αθροίσματα διαίρεσης. Για παράδειγμα, αν χρειαζόταν να χωρίσουν 3 ψωμιά σε 5 άτομα, θα χώριζαν πρώτα δύο από τα ψωμιά σε τρίτα και το τρίτο καρβέλι σε πέμπτα, μετά θα χώριζαν το υπόλοιπο ένα τρίτο από το δεύτερο καρβέλι σε πέντε κομμάτια. Έτσι, κάθε άτομο θα λάμβανε το ένα τρίτο συν ένα πέμπτο συν ένα δέκατο πέμπτο (το οποίο είναι συνολικά τρία πέμπτα, όπως θα περιμέναμε).

Οι Αιγύπτιοι προσέγγισαν το εμβαδόν ενός κύκλου χρησιμοποιώντας σχήματα των οποίων το εμβαδόν γνώριζαν. Παρατήρησαν ότι το εμβαδόν ενός κύκλου διαμέτρου 9 μονάδων, για παράδειγμα, ήταν πολύ κοντά στο εμβαδόν ενός τετραγώνου με πλευρές 8 μονάδων, έτσι ώστε το εμβαδόν των κύκλων άλλων διαμέτρων μπορούσε να ληφθεί πολλαπλασιάζοντας τη διάμετρο επί 8⁄ 9 και στη συνέχεια τετραγωνίζοντας το. Αυτό δίνει μια αποτελεσματική προσέγγιση του π ακριβείας σε λιγότερο από ένα τοις εκατό.
Οι ίδιες οι πυραμίδες είναι μια άλλη ένδειξη της πολυπλοκότητας των αιγυπτιακών μαθηματικών. Παραμερίζοντας τους ισχυρισμούς ότι οι πυραμίδες είναι οι πρώτες γνωστές δομές που παρατηρούν τη χρυσή αναλογία 1:1.618 (η οποία μπορεί να συνέβη για καθαρά αισθητικούς και όχι μαθηματικούς λόγους), υπάρχουν σίγουρα στοιχεία ότι γνώριζαν τον τύπο για τον όγκο μιας πυραμίδας – 1⁄3 φορές το ύψος επί το μήκος επί το πλάτος – καθώς και μιας κόλουρης ή κομμένης πυραμίδας.
Γνώριζαν επίσης, πολύ πριν από τον Πυθαγόρα, τον κανόνα ότι ένα τρίγωνο με πλευρές 3, 4 και 5 μονάδες δίνει τέλεια ορθή γωνία, και οι Αιγύπτιοι οικοδόμοι χρησιμοποιούσαν σχοινιά δεμένα με κόμπους σε διαστήματα 3, 4 και 5 μονάδων για να εξασφαλίσουν την ακριβή ορθή γωνία. γωνίες για την λιθοδομή τους (στην πραγματικότητα, το ορθογώνιο τρίγωνο 3-4-5 ονομάζεται συχνά «αιγυπτιακό»).

Published by