Τον 3ο αιώνα π.Χ., στον απόηχο των κατακτήσεων του Μεγάλου Αλεξάνδρου, μαθηματικές ανακαλύψεις άρχισαν επίσης να γίνονται στα όρια της ελληνικής αυτοκρατορίας.
Συγκεκριμένα, η Αλεξάνδρεια στην Αίγυπτο έγινε σπουδαίο κέντρο μάθησης υπό την ευεργετική κυριαρχία των Πτολεμαίων και η περίφημη Βιβλιοθήκη της σύντομα απέκτησε φήμη για να ανταγωνιστεί αυτήν της Αθηναϊκής Ακαδημίας. Οι θαμώνες της Βιβλιοθήκης ήταν αναμφισβήτητα οι πρώτοι επαγγελματίες επιστήμονες που πληρώθηκαν για την αφοσίωσή τους στην έρευνα. Μεταξύ των πιο γνωστών και πιο σημαντικών μαθηματικών που σπούδασαν και δίδαξαν στην Αλεξάνδρεια ήταν ο Ευκλείδης, ο Αρχιμήδης, ο Ερατοσθένης, ο Ήρων, ο Μενέλαος και ο Διόφαντος.
Στα τέλη του 4ου και στις αρχές του 3ου αιώνα π.Χ., ο Ευκλείδης ήταν ο μεγάλος χρονικογράφος των μαθηματικών της εποχής και ένας από τους πιο σημαντικούς δασκάλους στην ιστορία. Ουσιαστικά επινόησε την κλασική (Ευκλείδεια) γεωμετρία όπως την ξέρουμε. Ο Αρχιμήδης πέρασε το μεγαλύτερο μέρος της ζωής του στις Συρακούσες της Σικελίας, αλλά σπούδασε για λίγο στην Αλεξάνδρεια. Είναι ίσως περισσότερο γνωστός ως μηχανικός και εφευρέτης, αλλά, υπό το φως των πρόσφατων ανακαλύψεων, θεωρείται πλέον ένας από τους μεγαλύτερους καθαρούς μαθηματικούς όλων των εποχών. Ο Ερατοσθένης ο Αλεξανδρινός ήταν σχεδόν σύγχρονος του Αρχιμήδη τον 3ο αιώνα π.Χ. Μαθηματικός, αστρονόμος και γεωγράφος, επινόησε το πρώτο σύστημα γεωγραφικού πλάτους και μήκους και υπολόγισε την περιφέρεια της γης με αξιοσημείωτο βαθμό ακρίβειας. Ως μαθηματικός, η μεγαλύτερη κληρονομιά του είναι ο αλγόριθμος «Κόσκινο του Ερατοσθένη» για την αναγνώριση πρώτων αριθμών.
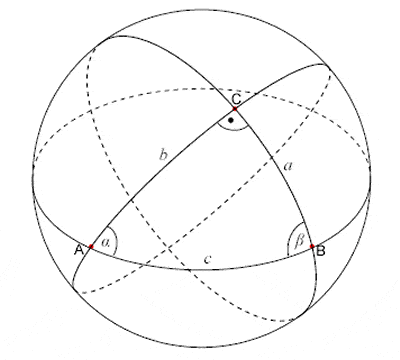
Σφαιρικό Τρίγωνο
Δεν είναι γνωστό πότε ακριβώς κάηκε η μεγάλη Βιβλιοθήκη της Αλεξάνδρειας, αλλά η Αλεξάνδρεια παρέμεινε σημαντικό πνευματικό κέντρο για μερικούς αιώνες. Τον 1ο αιώνα π.Χ., ο Ήρων ήταν ένας άλλος μεγάλος Αλεξανδρινός εφευρέτης, πιο γνωστός στους μαθηματικούς κύκλους για τα Ηρωνιακά τρίγωνα (τρίγωνα με ακέραιες πλευρές και ακέραιο εμβαδόν), τον τύπο του Ήρωνα για την εύρεση του εμβαδού ενός τριγώνου από τα μήκη των πλευρών του και τη “Μέθοδο του Ήρωνα” για τον επαναληπτικό υπολογισμό μιας τετραγωνικής ρίζας. Ήταν επίσης ο πρώτος μαθηματικός που αντιμετώπισε τουλάχιστον την ιδέα του √-1 (αν και δεν είχε ιδέα πώς να το αντιμετωπίσει, κάτι που έπρεπε να περιμένει τον Tartaglia και τον Cardano τον 16ο αιώνα).
Ο Μενέλαος ο Αλεξανδρεύς, που έζησε τον 1ο – 2ο αιώνα μ.Χ., ήταν ο πρώτος που αναγνώρισε τη γεωδαισία σε μια καμπύλη επιφάνεια ως τα φυσικά ανάλογα των ευθειών γραμμών σε ένα επίπεδο επίπεδο. Το βιβλίο του «Σφαιρική» ασχολήθηκε με τη γεωμετρία της σφαίρας και την εφαρμογή της σε αστρονομικές μετρήσεις και υπολογισμούς και εισήγαγε την έννοια του σφαιρικού τριγώνου (ένα σχήμα που σχηματίζεται από τρία μεγάλα τόξα κύκλων, τα οποία ονόμασε «τρίπλευρα»).
Τον 3ο αιώνα μ.Χ., ο Διόφαντος από την Αλεξάνδρεια ήταν ο πρώτος που αναγνώρισε τα κλάσματα ως αριθμούς και θεωρείται πρώιμος καινοτόμος στον τομέα αυτού που αργότερα θα γίνει γνωστό ως άλγεβρα. Εφαρμόστηκε σε μερικά αρκετά πολύπλοκα αλγεβρικά προβλήματα, συμπεριλαμβανομένου αυτού που είναι σήμερα γνωστό ως Διοφαντική Ανάλυση, που ασχολείται με την εύρεση ακέραιων λύσεων σε είδη προβλημάτων που οδηγούν σε εξισώσεις με πολλούς αγνώστους (Διοφαντικές εξισώσεις). Η «Αριθμητική» του Διόφαντου, μια συλλογή προβλημάτων που δίνει αριθμητικές λύσεις τόσο καθορισμένων όσο και απροσδιόριστων εξισώσεων, ήταν το πιο σημαντικό έργο για την άλγεβρα σε όλα τα ελληνικά μαθηματικά και τα προβλήματά του ασκούσαν το μυαλό πολλών από τους καλύτερους μαθηματικούς του κόσμου για μεγάλο μέρος του επόμενου δύο χιλιετίες.
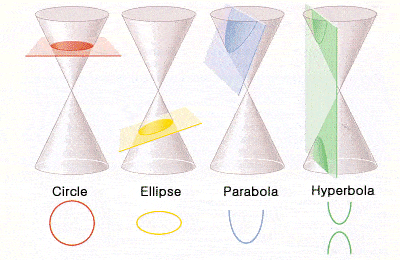
Κωνικές τομές του Απολλώνιου
Όμως η Αλεξάνδρεια δεν ήταν το μόνο κέντρο μάθησης στην ελληνική αυτοκρατορία. Θα πρέπει επίσης να αναφερθεί ο Απολλώνιος ο Περγαίος, του οποίου η εργασία στα τέλη του 3ου αιώνα π.Χ. σχετικά με τη γεωμετρία (και, ειδικότερα, τις κωνικές τομές) είχε μεγάλη επιρροή στους μεταγενέστερους Ευρωπαίους μαθηματικούς. Ήταν ο Απολλώνιος που έδωσε στην έλλειψη, την παραβολή και την υπερβολή τα ονόματα με τα οποία τα γνωρίζουμε και έδειξε πώς θα μπορούσαν να προέρχονται από διαφορετικά τμήματα μέσω ενός κώνου.
Ο Ίππαρχος, ο οποίος ήταν επίσης από την ελληνιστική Ανατολία και έζησε τον 2ο αιώνα π.Χ., ήταν ίσως ο μεγαλύτερος από όλους τους αρχαίους αστρονόμους. Αναβίωσε τη χρήση των αριθμητικών τεχνικών που αναπτύχθηκαν για πρώτη φορά από τους Χαλδαίους και τους Βαβυλώνιους, και συνήθως πιστώνεται με τις απαρχές της τριγωνομετρίας. Υπολόγισε (με αξιοσημείωτη ακρίβεια για την εποχή) την απόσταση της σελήνης από τη γη μετρώντας τα διάφορα μέρη της σελήνης ορατά σε διαφορετικές τοποθεσίες και υπολογίζοντας την απόσταση χρησιμοποιώντας τις ιδιότητες των τριγώνων. Συνέχισε δημιουργώντας τον πρώτο πίνακα συγχορδιών (μήκη πλευρών που αντιστοιχούν σε διαφορετικές γωνίες τριγώνου). Ωστόσο, την εποχή του μεγάλου Αλεξανδρινού αστρονόμου Πτολεμαίου τον 2ο αιώνα μ.Χ., η ελληνική γνώση των αριθμητικών διαδικασιών είχε προχωρήσει στο σημείο που ο Πτολεμαίος μπόρεσε να συμπεριλάβει στην «Αλμαγέστη» έναν πίνακα τριγωνομετρικών χορδών σε κύκλο για βήματα ενός τετάρτου της μοίρας, το οποίο (αν και εκφράζεται στο εξηνταδικό Βαβυλωνιακό σύστημα) είναι ακριβές με περίπου πέντε δεκαδικά ψηφία.
Από τα μέσα του 1ου αιώνα π.Χ. και μετά, ωστόσο, οι Ρωμαίοι είχαν σφίξει τον έλεγχο της παλαιάς ελληνικής αυτοκρατορίας. Οι Ρωμαίοι δεν είχαν κανένα ενδιαφέρον για τα καθαρά μαθηματικά, μόνο για τις πρακτικές τους εφαρμογές, και το χριστιανικό καθεστώς που τα ακολούθησε ακόμη λιγότερο. Το τελευταίο χτύπημα στην ελληνιστική μαθηματική κληρονομιά στην Αλεξάνδρεια μπορεί να φανεί στη φιγούρα της Υπατίας, της πρώτης καταγεγραμμένης γυναίκας μαθηματικού, και μιας διάσημης δασκάλας που είχε γράψει μερικά αξιοσέβαστα σχόλια για τον Διόφαντο και τον Απολλώνιο. Την έσυρε στο θάνατο ο χριστιανικός όχλος το 415 μ.Χ.

Published by