Το Σουμέρ (περιοχή της Μεσοποταμίας, το σύγχρονο Ιράκ) ήταν η γενέτειρα της γραφής, του τροχού, της γεωργίας, της αψίδας, του άροτρου, της άρδευσης και πολλών άλλων καινοτομιών, και συχνά αναφέρεται ως το λίκνο του πολιτισμού. Οι Σουμέριοι ανέπτυξαν το παλαιότερο γνωστό σύστημα γραφής – ένα εικονογραφικό σύστημα γραφής γνωστό ως σφηνοειδή γραφή, χρησιμοποιώντας σφηνοειδείς χαρακτήρες εγγεγραμμένους σε ψημένες πήλινες πλάκες – και αυτό σημαίνει ότι έχουμε στην πραγματικότητα περισσότερη γνώση των αρχαίων Σουμερίων και Βαβυλωνιακών μαθηματικών παρά των πρώιμων αιγυπτιακών μαθηματικών. Πράγματι, έχουμε ακόμη και αυτό που φαίνεται να είναι σχολικές ασκήσεις σε αριθμητικά και γεωμετρικά προβλήματα.
Όπως και στην Αίγυπτο, τα Σουμεριακά μαθηματικά αναπτύχθηκαν αρχικά σε μεγάλο βαθμό ως απάντηση στις γραφειοκρατικές ανάγκες, όταν εγκαταστάθηκε ο πολιτισμός τους και ανέπτυξε τη γεωργία (πιθανώς ήδη από την 6η χιλιετία π.Χ.) για τη μέτρηση των οικοπέδων, τη φορολόγηση των ατόμων κ.λπ. οι Σουμέριοι και οι Βαβυλώνιοι χρειαζόταν να περιγράψουν αρκετά μεγάλους αριθμούς καθώς προσπαθούσαν να χαράξουν την πορεία του νυχτερινού ουρανού και να αναπτύξουν το εξελιγμένο σεληνιακό τους ημερολόγιο.
Ήταν ίσως οι πρώτοι άνθρωποι που ανέθεσαν σύμβολα σε ομάδες αντικειμένων σε μια προσπάθεια να κάνουν την περιγραφή μεγαλύτερων αριθμών ευκολότερη. Μεταπήδησαν από τη χρήση ξεχωριστών σημείων ή συμβόλων για να αναπαραστήσουν στάχυα σιταριού, βάζα με λάδι κ.λπ., στην πιο αφηρημένη χρήση ενός συμβόλου για συγκεκριμένους αριθμούς.
Ξεκινώντας ήδη από την 4η χιλιετία π.Χ., άρχισαν να χρησιμοποιούν έναν μικρό πήλινο κώνο για να αναπαραστήσουν το ένα, μια πήλινη μπάλα για το δέκα και έναν μεγάλο κώνο για το εξήντα. Κατά τη διάρκεια της τρίτης χιλιετίας, αυτά τα αντικείμενα αντικαταστάθηκαν από ισοδύναμα σφηνοειδούς γραφής, έτσι ώστε οι αριθμοί να μπορούν να γράφονται με την ίδια γραφίδα που χρησιμοποιούνταν για τις λέξεις του κειμένου. Ένα στοιχειώδες μοντέλο του άβακα ήταν πιθανώς σε χρήση στη Σουμερία ήδη από το 2700 – 2300 π.Χ.
Σύστημα Αριθμών Σουμερίων και Βαβυλωνίων: Βάση 60
Τα Σουμεριακά και Βαβυλωνιακά μαθηματικά βασίστηκαν σε ένα εξηνταδικό (με βάση το 60), αριθμητικό σύστημα, το οποίο μπορούσε να μετρηθεί φυσικά χρησιμοποιώντας τις δώδεκα αρθρώσεις από το ένα χέρι και τα πέντε δάχτυλα από την άλλη. Σε αντίθεση με εκείνους των Αιγυπτίων, των Ελλήνων και των Ρωμαίων, οι Βαβυλωνιακοί αριθμοί χρησιμοποιούσαν ένα πραγματικό σύστημα τοποαξίας, όπου τα ψηφία που γράφονταν στην αριστερή στήλη αντιπροσώπευαν μεγαλύτερες τιμές, όπως στο σύγχρονο δεκαδικό σύστημα, αν και φυσικά χρησιμοποιούν τη βάση 60 όχι τη βάση 10. Έτσι, ο αριθμός 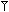
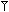
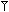 στο Βαβυλωνιακό σύστημα αντιπροσώπευε 3.600 συν 60 συν 1, ή 3.661. Επίσης, για την αναπαράσταση των αριθμών 1 – 59 σε κάθε τοποαξία, χρησιμοποιήθηκαν δύο διακριτά σύμβολα, ένα σύμβολο μονάδας (
στο Βαβυλωνιακό σύστημα αντιπροσώπευε 3.600 συν 60 συν 1, ή 3.661. Επίσης, για την αναπαράσταση των αριθμών 1 – 59 σε κάθε τοποαξία, χρησιμοποιήθηκαν δύο διακριτά σύμβολα, ένα σύμβολο μονάδας (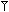 ) και ένα σύμβολο δέκα (
) και ένα σύμβολο δέκα (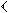 ) που συνδυάστηκαν με παρόμοιο τρόπο με το γνωστό σύστημα των ρωμαϊκών αριθμών ( π.χ. το 23 θα εμφανιζόταν ως
) που συνδυάστηκαν με παρόμοιο τρόπο με το γνωστό σύστημα των ρωμαϊκών αριθμών ( π.χ. το 23 θα εμφανιζόταν ως 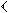
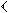
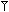
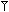
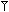 ). Έτσι, ο αριθμός
). Έτσι, ο αριθμός 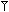
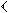
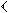
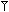
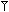
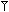 αντιπροσωπεύει το 60 συν 23, ή το 83. Ωστόσο, ο αριθμός 60 αντιπροσωπευόταν με το ίδιο σύμβολο με τον αριθμό 1 και, επειδή τους έλειπε το ισοδύναμο της υποδιαστολής, η πραγματική θέση ενός συμβόλου έπρεπε να γίνει αντιληπτή από τα συμφραζόμενα.
αντιπροσωπεύει το 60 συν 23, ή το 83. Ωστόσο, ο αριθμός 60 αντιπροσωπευόταν με το ίδιο σύμβολο με τον αριθμό 1 και, επειδή τους έλειπε το ισοδύναμο της υποδιαστολής, η πραγματική θέση ενός συμβόλου έπρεπε να γίνει αντιληπτή από τα συμφραζόμενα.
Έχει υποτεθεί ότι η πρόοδος της Βαβυλωνίας στα μαθηματικά διευκολύνθηκε πιθανώς από το γεγονός ότι το 60 έχει πολλούς διαιρέτες (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 και 60 – στην πραγματικότητα, το 60 είναι ο μικρότερος ακέραιος που διαιρείται με όλους τους ακέραιους αριθμούς από το 1 έως το 6) και η συνεχιζόμενη σύγχρονη χρήση των 60 δευτερολέπτων σε ένα λεπτό, 60 λεπτών σε μια ώρα και 360 (60 x 6) μοιρών σε έναν κύκλο, είναι όλα μαρτυρίες το αρχαίο βαβυλωνιακό σύστημα. Είναι για παρόμοιους λόγους που το 12 (το οποίο έχει διαιρέτες 1, 2, 3, 4 και 6) ήταν τόσο δημοφιλές πολλαπλάσιο ιστορικά (π.χ. 12 μήνες, 12 ίντσες, 12 πένες, 2 x 12 ώρες, κ.λπ.).
Οι Βαβυλώνιοι ανέπτυξαν επίσης μια άλλη επαναστατική μαθηματική έννοια, κάτι άλλο που δεν είχαν οι Αιγύπτιοι, οι Έλληνες και οι Ρωμαίοι, έναν κυκλικό χαρακτήρα για το μηδέν, αν και το σύμβολό του ήταν στην πραγματικότητα περισσότερο ένα σύμβολο θέσης παρά ένας αριθμός από μόνος του.
Βαβυλωνιακά πήλινα δισκία
Έχουμε στοιχεία για την ανάπτυξη ενός πολύπλοκου συστήματος μετρολογίας στο Σούμερ από περίπου το 3000 π.Χ., και πίνακες πολλαπλασιασμού και μοιρασιάς (διαίρεσης), πίνακες τετραγώνων, τετραγωνικών ριζών και κυβικών ριζών, γεωμετρικών ασκήσεων και προβλημάτων διαίρεσης από περίπου το 2600 π.Χ. και μετά. Οι μεταγενέστερες βαβυλωνιακές πινακίδες που χρονολογούνται από το 1800 έως το 1600 περίπου π.Χ. καλύπτουν θέματα τόσο ποικίλα όπως κλάσματα, άλγεβρα, μεθόδους επίλυσης γραμμικών, τετραγωνικών, ακόμη και μερικών κυβικών εξισώσεων, και τον υπολογισμό κανονικών αμοιβαίων ζευγών (ζεύγη αριθμών που πολλαπλασιάζονται μαζί για να δώσουν το 60). Μια βαβυλωνιακή ταμπλέτα δίνει μια προσέγγιση για το √2 με ακρίβεια έως πέντε δεκαδικών ψηφίων. Άλλες πινακίδες, απαριθμούν τα τετράγωνα των αριθμών μέχρι το 59, τους κύβους των αριθμών μέχρι το 32 καθώς και πίνακες σύνθετου ενδιαφέροντος. Άλλη μια, δίνει μια εκτίμηση για το π=3 1/8=3.125, μια καλή προσέγγιση της πραγματικής τιμής του 3.1416.
Η ιδέα των τετραγωνικών αριθμών και των δευτεροβάθμιων εξισώσεων (όπου η άγνωστη ποσότητα πολλαπλασιάζεται με τον εαυτό της) προέκυψε φυσικά στο πλαίσιο της μέτρησης της γης, και οι βαβυλωνιακές μαθηματικές ταμπλέτες μας δίνουν την πρώτη απόδειξη της επίλυσης των δευτεροβάθμιων εξισώσεων. Η βαβυλωνιακή προσέγγιση για την επίλυσή τους περιστρέφεται συνήθως γύρω από ένα είδος γεωμετρικού παιχνιδιού τεμαχισμού και αναδιάταξης σχημάτων, αν και εμφανίζεται επίσης η χρήση άλγεβρας και δευτεροβάθμιων εξισώσεων.
Οι Βαβυλώνιοι χρησιμοποιούσαν γεωμετρικά σχήματα στα κτίρια και το σχέδιό τους και σε ζάρια για τα ψυχαγωγικά παιχνίδια που ήταν τόσο δημοφιλή στην κοινωνία τους, όπως το αρχαίο παιχνίδι του τάβλι. Η γεωμετρία τους επεκτάθηκε στον υπολογισμό των εμβαδών των ορθογωνίων, τριγώνων και τραπεζοειδών, καθώς και των όγκων απλών σχημάτων όπως τούβλων και κυλίνδρων (αν και όχι πυραμίδων).
Πήλινη ταμπλέτα Plimpton 322
Η περίφημη και αμφιλεγόμενη πήλινη πινακίδα Plimpton 322, που πιστεύεται ότι χρονολογείται γύρω στο 1800 π.Χ., υποδηλώνει ότι οι Βαβυλώνιοι μπορεί κάλλιστα να γνώριζαν το μυστικό των ορθογώνιων τριγώνων (ότι το τετράγωνο της υποτείνουσας ισούται με το άθροισμα του τετραγώνου των άλλων δύο πλευρών) πολλούς αιώνες πριν τον Έλληνα Πυθαγόρα. Η ταμπλέτα φαίνεται να απαριθμεί 15 τέλεια πυθαγόρεια τρίγωνα με πλευρές ακέραιους αριθμούς, αν και ορισμένοι ισχυρίζονται ότι ήταν απλώς ακαδημαϊκές ασκήσεις και όχι σκόπιμες εκδηλώσεις των Πυθαγόρειων τριάδων.